Description of the course
The course demonstrates how mathematical concepts and techniques can be applied to analyze and solve problems in the field of computer networking. Mathematics plays a crucial role in networking as it provides the foundation for various aspects of network design, analysis, and optimization. It teaches students topics to study an efficient programming language and algorithm about graph theory and planarity. By studying Mathematics in Networking, students gain the following:
- Understanding network topology. Mathematics helps in studying and representing the structure and connectivity of computer networks. Graph theory, a branch of mathematics, is used to model and analyze network topologies, including concepts such as nodes, edges, connectivity, and paths.
- Analyzing network performance. Mathematics is used to analyze the performance of computer networks, including metrics such as throughput, latency, and packet loss. Probability theory and queuing theory are applied to model and analyze network traffic and performance, allowing network administrators to optimize network resources and improve overall performance.
- Routing and switching. Mathematics is used to develop algorithms for routing and switching in computer networks. Optimization techniques, such as linear programming and graph theory, are applied to find the most efficient paths for data packets to traverse the network, minimizing delays and congestion.
- Data analysis. Mathematics is used to analyze network data, such as traffic patterns, user behavior, and network performance metrics. Statistical analysis techniques, such as regression analysis and hypothesis testing, are applied to identify trends, anomalies, and patterns in network data, enabling network administrators to make informed decisions and troubleshoot network issues.
Description of the participants
Participants are enrolled full-time in the Bachelor’s of Computer Science program. A total of 5 students attended the course in semester 1 of academic year 2022 – 2023 in a preliminary offering of the course.
Description of gamified design thinking activities
Students participated in weekly meetings. At the beginning of the class, the course coordinator provided a 30-minutes briefing on design thinking. The students met their team members on-line. Course material, including design thinking activities sheets and templates, was shared through the MSTeams® platform.
Students worked in a group of 5 individuals. Their work was organized as follows:
Step 1. Understanding the problem.
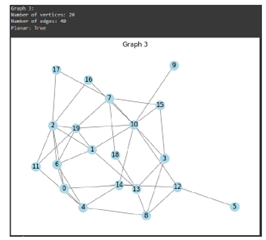
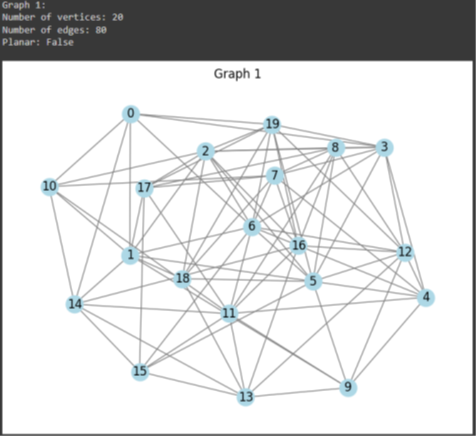
Students performed research for gaining a clear understanding of the problem at hand, which was determining whether a randomly generated simple graph is planar or not. They familiarized themselves with the concept of planarity and the criteria that define a planar graph.
Step 2. Research and information gathering.
Students conducted research to understand the properties and characteristics of planar graphs. They explored existing algorithms and techniques used to determine planarity. This step helped students to gather information and insights that would inform the design thinking process.
Step 3. Ideation.
Once they had developed a good understanding of the problem, students started generating ideas for determining planarity. They considered different approaches, algorithms, and techniques that could be applied to solve the problem. They brainstormed with others to come up with a variety of potential solutions.
Step 4. Prototyping solutions.
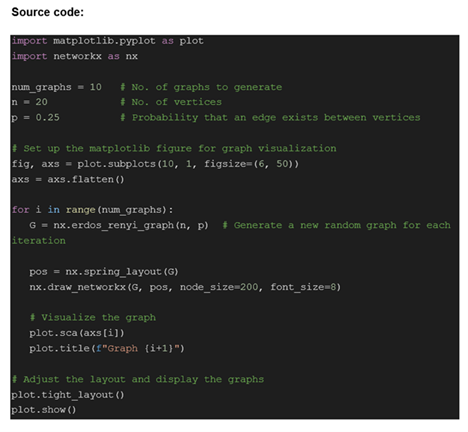
Students selected one or more of the ideas generated and created prototypes or models to test them. This involved implementing algorithms or using simulation tools to analyze randomly generated graphs and determine their planarity. The prototypes were designed in a manner that allowed taking input in the form of a graph and providing an output indicating whether the graph was planar or not.
Step 5. Testing and iterating.
Students tested the prototypes using various randomly generated simple graphs to verify their accuracy and effectiveness in determining planarity. They evaluated the results and iterated on the prototypes when necessary. They collected feedback from users or experts in the field to further refine the solution.
Step 6. Refining and implementing.
Based on the feedback received and the results of testing, students refined the prototypes and developed a final solution. This involved improving the efficiency or accuracy of the algorithm, enhancing the user interface, or addressing any limitations or issues identified during testing.
Step 7. Validating and deploying.
Students validated the final solution by testing it with a diverse set of randomly generated simple graphs. They ensured that it consistently provided accurate results in determining planarity. They deployed the validated solution in practical scenarios.